lc112. 路径总和(MD)
给你二叉树的根节点 root 和一个表示目标和的整数 targetSum 。判断该树中是否存在 根节点到叶子节点 的路径,这条路径上所有节点值相加等于目标和 targetSum 。如果存在,返回 true ;否则,返回 false 。
叶子节点 是指没有子节点的节点。
示例 1:

输入:root = [5,4,8,11,null,13,4,7,2,null,null,null,1], targetSum = 22
输出:true
解释:等于目标和的根节点到叶节点路径如上图所示。
|
示例 2:

输入:root = [1,2,3], targetSum = 5
输出:false
解释:树中存在两条根节点到叶子节点的路径:
(1 --> 2): 和为 3
(1 --> 3): 和为 4
不存在 sum = 5 的根节点到叶子节点的路径。
|
示例 3:
输入:root = [], targetSum = 0
输出:false
解释:由于树是空的,所以不存在根节点到叶子节点的路径。
|
提示:
- 树中节点的数目在范围
[0, 5000] 内 -1000 <= Node.val <= 1000-1000 <= targetSum <= 1000
左右子树递归地查找
class Solution {
public boolean hasPathSum(TreeNode root, int targetSum) {
if (root == null) {
return false;
}
if (root.left == null && root.right == null && root.val == targetSum) {
return true;
}
return hasPathSum(root.left, targetSum - root.val) || hasPathSum(root.right, targetSum - root.val);
}
}
|
lc129. 求根节点到叶节点数字之和(MD)
给你一个二叉树的根节点 root ,树中每个节点都存放有一个 0 到 9 之间的数字。
每条从根节点到叶节点的路径都代表一个数字:
- 例如,从根节点到叶节点的路径
1 -> 2 -> 3 表示数字 123 。
计算从根节点到叶节点生成的 所有数字之和 。
叶节点 是指没有子节点的节点。
示例 1:

输入:root = [1,2,3]
输出:25
解释:
从根到叶子节点路径 1->2 代表数字 12
从根到叶子节点路径 1->3 代表数字 13
因此,数字总和 = 12 + 13 = 25
|
示例 2:

输入:root = [4,9,0,5,1]
输出:1026
解释:
从根到叶子节点路径 4->9->5 代表数字 495
从根到叶子节点路径 4->9->1 代表数字 491
从根到叶子节点路径 4->0 代表数字 40
因此,数字总和 = 495 + 491 + 40 = 1026
|
提示:
- 树中节点的数目在范围
[1, 1000] 内 0 <= Node.val <= 9- 树的深度不超过
10
深搜即可
class Solution {
public int sumNumbers(TreeNode root) {
return dfs(root, 0);
}
private int dfs(TreeNode root, int prevsum) {
if (root == null) {
return 0;
}
int sum = prevsum * 10 + root.val;
if (root.left == null && root.right == null) {
return sum;
} else {
return dfs(root.left, sum) + dfs(root.right, sum);
}
}
}
|
lc124. 二叉树中的最大路径和(HD)
二叉树中的 路径 被定义为一条节点序列,序列中每对相邻节点之间都存在一条边。同一个节点在一条路径序列中 至多出现一次 。该路径 至少包含一个 节点,且不一定经过根节点。
路径和 是路径中各节点值的总和。
给你一个二叉树的根节点 root ,返回其 最大路径和 。
示例 1:

输入:root = [1,2,3]
输出:6
解释:最优路径是 2 -> 1 -> 3 ,路径和为 2 + 1 + 3 = 6
|
示例 2:

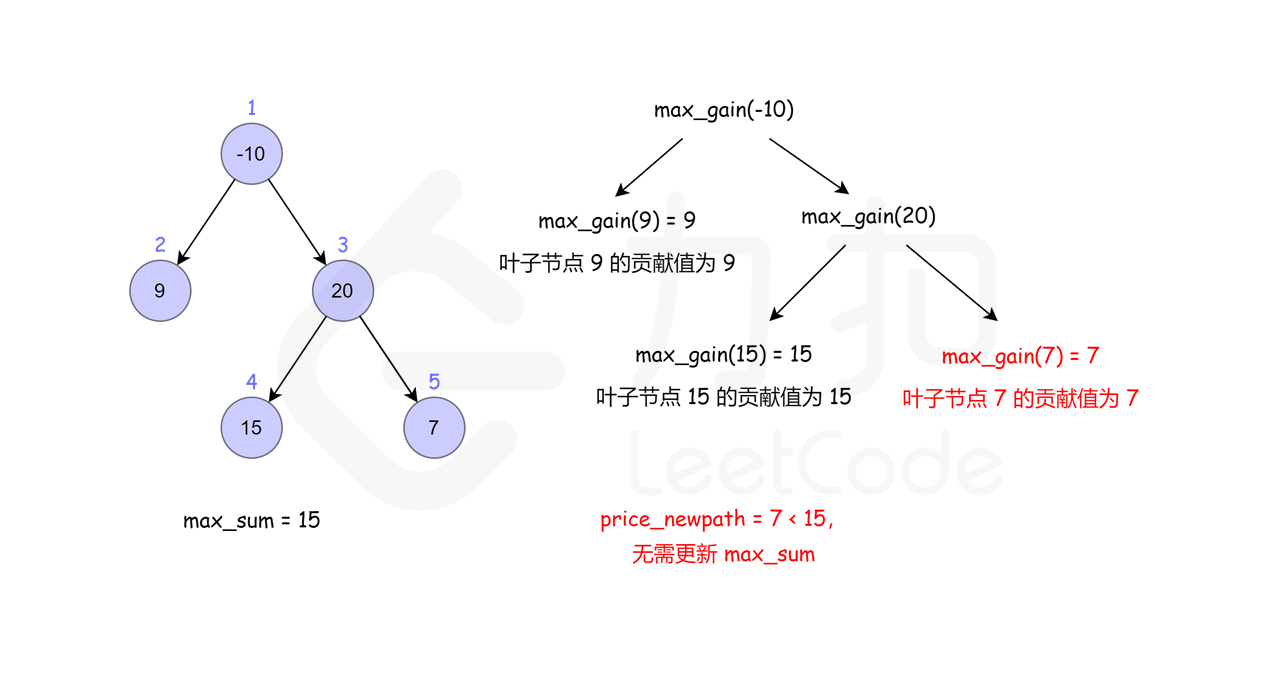
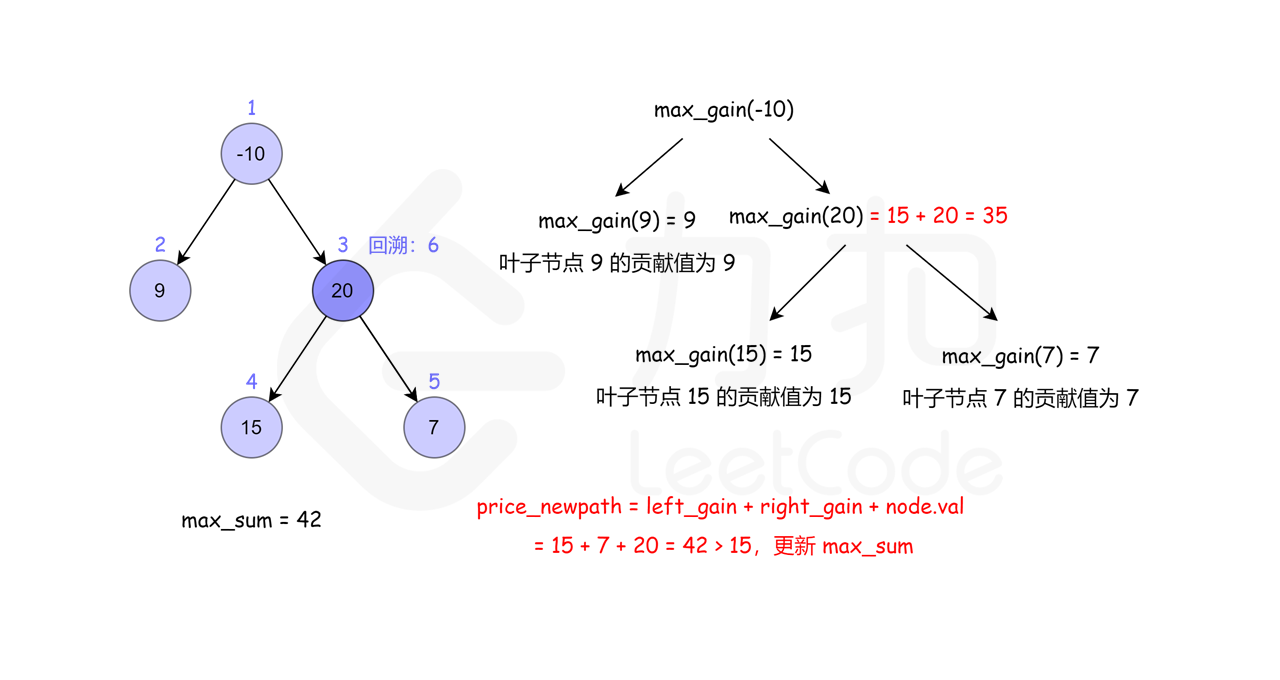
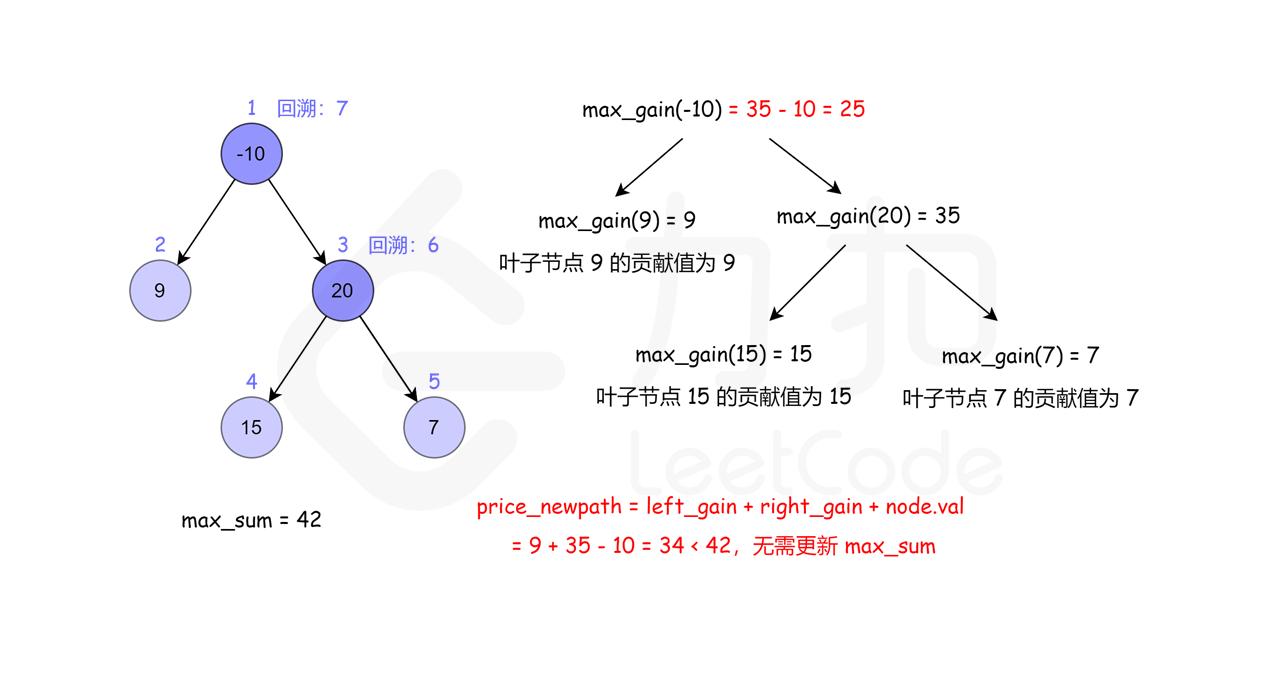
输入:root = [-10,9,20,null,null,15,7]
输出:42
解释:最优路径是 15 -> 20 -> 7 ,路径和为 15 + 20 + 7 = 42
|
提示:
- 树中节点数目范围是
[1, 3 * 104] -1000 <= Node.val <= 1000
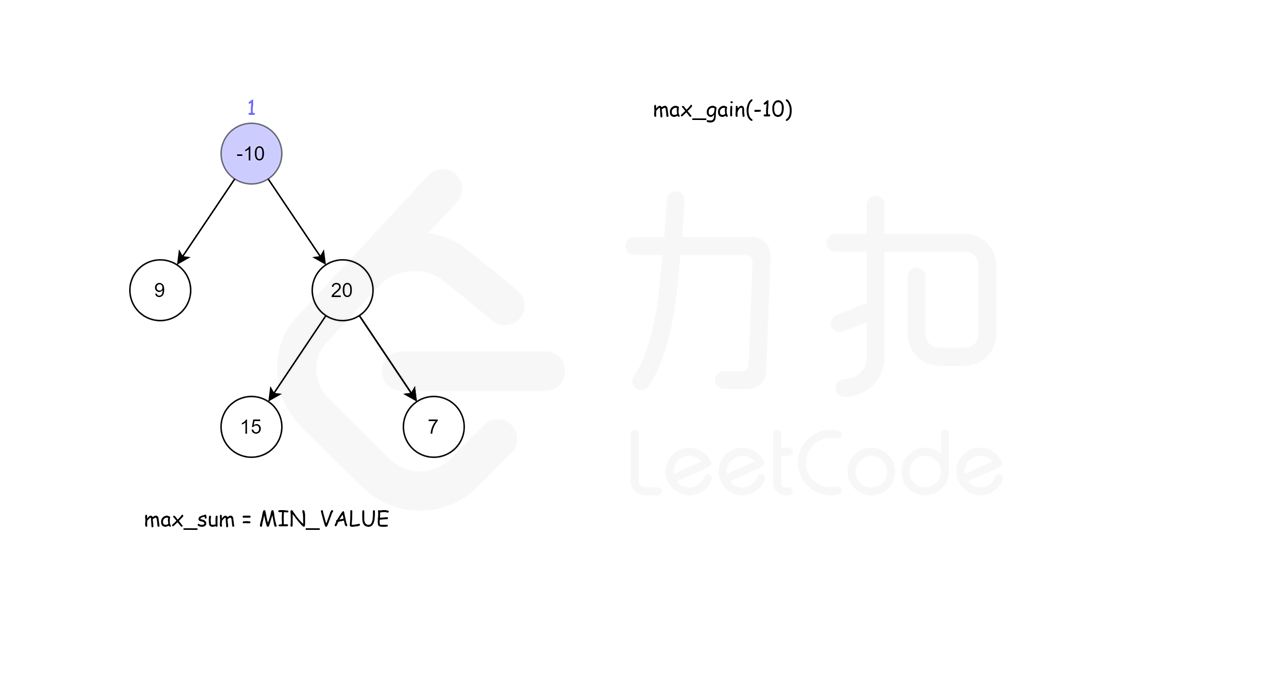
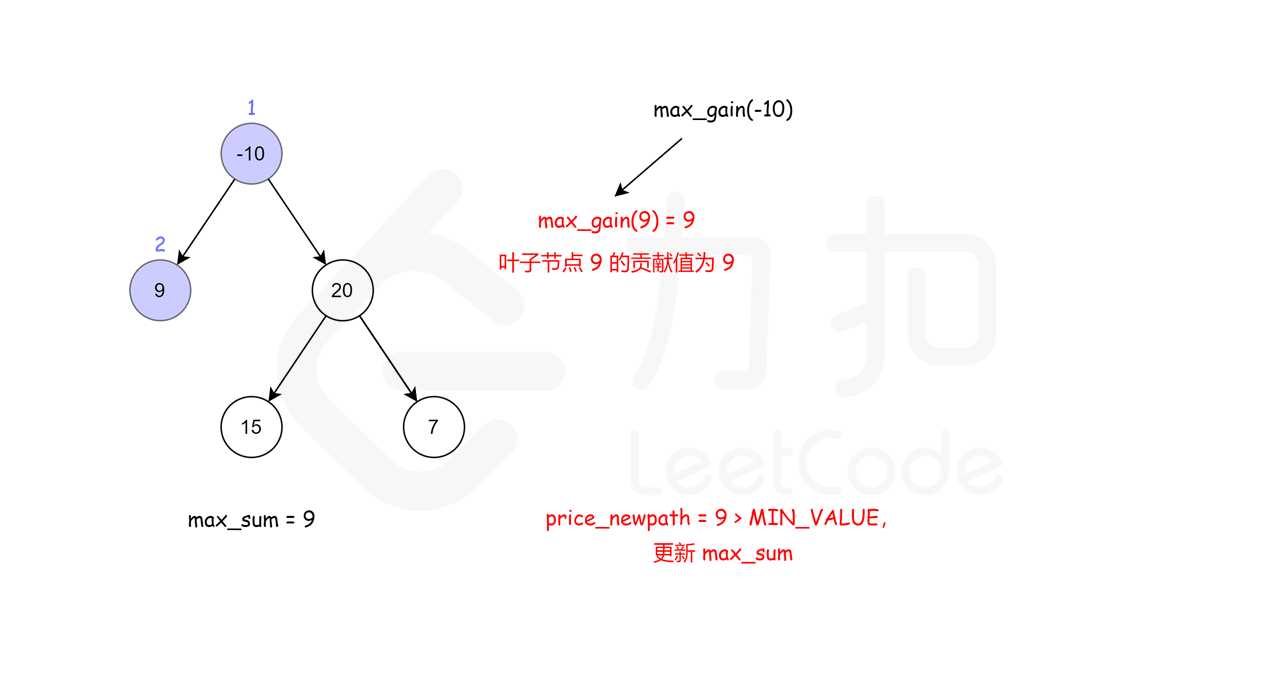
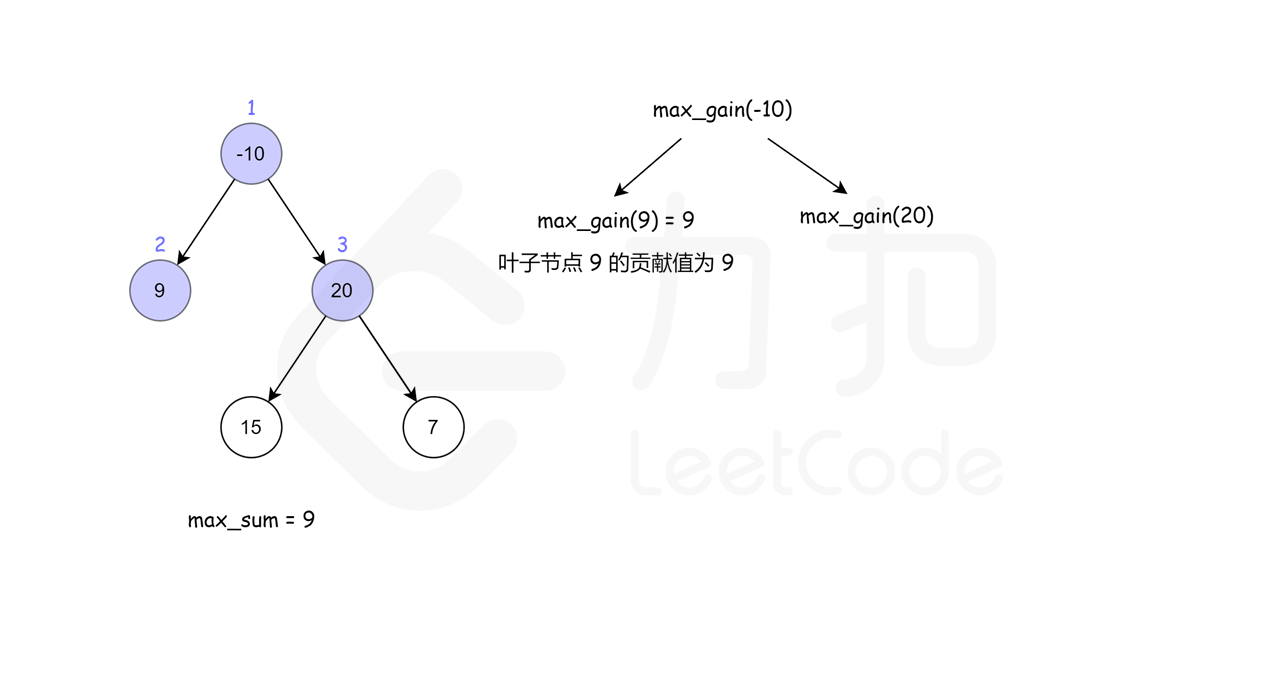
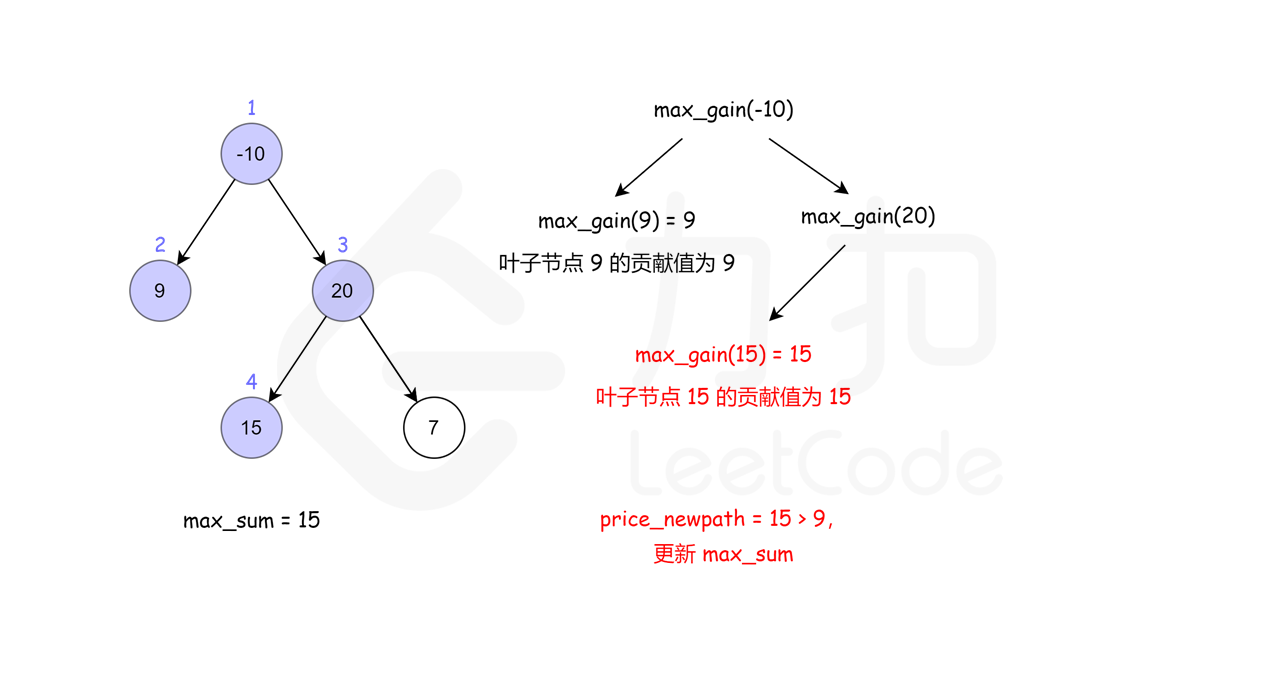
左右子树,递归查找
这里借用一下leetcode官方题解的配图, 看了配图就很容易理解了







class Solution {
int maxSum = Integer.MIN_VALUE;
public int maxPathSum(TreeNode root) {
maxGain(root);
return maxSum;
}
private int maxGain(TreeNode root) {
if (root == null) {
return 0;
}
int leftGain = Math.max(maxGain(root.left), 0);
int rightGain = Math.max(maxGain(root.right), 0);
int priceNewPath = root.val + leftGain + rightGain;
maxSum = Math.max(maxSum, priceNewPath);
return root.val + Math.max(leftGain, rightGain);
}
}
|
lc222. 完全二叉树的节点个数(EZ)
给你一棵 完全二叉树 的根节点 root ,求出该树的节点个数。
完全二叉树 的定义如下:在完全二叉树中,除了最底层节点可能没填满外,其余每层节点数都达到最大值,并且最下面一层的节点都集中在该层最左边的若干位置。若最底层为第 h 层,则该层包含 1~ 2h 个节点。
示例 1:

输入:root = [1,2,3,4,5,6]
输出:6
|
示例 2:
示例 3:
提示:
- 树中节点的数目范围是
[0, 5 * 104] 0 <= Node.val <= 5 * 104- 题目数据保证输入的树是 完全二叉树
**进阶:**遍历树来统计节点是一种时间复杂度为 O(n) 的简单解决方案。你可以设计一个更快的算法吗?
最简单的方法:层级遍历,遍历一层,统计这一层的节点个数,然后就能计算出总节点个数
但是这种方法没有利用好完全二叉树的特性
当完全二叉树的底层节点全部填满时,完全二叉树就是满二叉树,根据数据结构相关知识,假设满二叉树高度为n , 那么满二叉树的节点数是2n−1
利用这个特性,就能很快计算出完全二叉树的节点个数——左右两边分别计算高度,假如高度相等就能用二叉树高度直接计算节点个数;假如不等就左右子树分别递归计算高度
class Solution {
public int countNodes(TreeNode root) {
if (root == null) {
return 0;
}
TreeNode leftNode = root.left;
TreeNode rightNode = root.right;
int leftCnt = 0, rightCnt = 0;
while (leftNode != null) {
leftNode = leftNode.left;
leftCnt++;
}
while (rightNode != null) {
rightNode = rightNode.right;
rightCnt++;
}
if (leftCnt == rightCnt) {
return (2 << leftCnt) - 1;
}
return countNodes(root.left) + countNodes(root.right) + 1;
}
}
|