lc236. 二叉树的最近公共祖先(MD)
百度百科中最近公共祖先的定义为:“对于有根树 T 的两个节点 p、q,最近公共祖先表示为一个节点 x,满足 x 是 p、q 的祖先且 x 的深度尽可能大(一个节点也可以是它自己的祖先)。”
示例 1:

输入:root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1
输出:3
解释:节点 5 和节点 1 的最近公共祖先是节点 3 。
|
示例 2:

输入:root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 4
输出:5
解释:节点 5 和节点 4 的最近公共祖先是节点 5 。因为根据定义最近公共祖先节点可以为节点本身。
|
示例 3:
输入:root = [1,2], p = 1, q = 2
输出:1
|
提示:
- 树中节点数目在范围
[2, 10^5] 内。 -10^9 <= Node.val <= 10^9- 所有
Node.val 互不相同 。 p != qp 和 q 均存在于给定的二叉树中。
左右两边递归遍历二叉树
如果左右两边遍历结果都不为空(意味着一个节点在左子树, 一个节点在右子树), 那么最近的公共祖先就应该是当前的root节点. 反之, 如果有一侧是空的, 说明两个节点全部在另外一侧, 就得看另外一侧的结果了
class Solution {
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
if (root == null || root == p || root == q) {
return root;
}
TreeNode left = lowestCommonAncestor(root.left, p, q);
TreeNode right = lowestCommonAncestor(root.right, p, q);
if (left != null && right != null) {
return root;
}
if (left == null) {
return right;
}
return left;
}
}
|
lc199. 二叉树的右视图(MD)
给定一个二叉树的 根节点 root,想象自己站在它的右侧,按照从顶部到底部的顺序,返回从右侧所能看到的节点值。
示例 1:

输入: [1,2,3,null,5,null,4]
输出: [1,3,4]
|
示例 2:
示例 3:
提示:
- 二叉树的节点个数的范围是
[0,100] -100 <= Node.val <= 100
二叉树层次遍历即可, 每遍历一层到最后一个节点就把这个节点的val值存进List
class Solution {
public List<Integer> rightSideView(TreeNode root) {
List<Integer> res = new ArrayList<>();
if (root == null) {
return res;
}
Queue<TreeNode> que = new LinkedList<>();
que.offer(root);
while (!que.isEmpty()) {
int len = que.size();
for (int i = 0; i < len; i++) {
TreeNode node = que.poll();
if (i == len - 1) {
res.add(node.val);
}
if (node.left != null) {
que.offer(node.left);
}
if (node.right != null) {
que.offer(node.right);
}
}
}
return res;
}
}
|
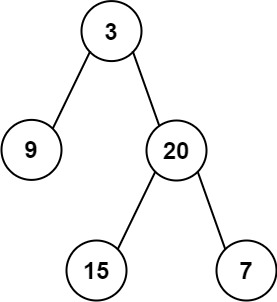
lc637. 二叉树的层平均值(EZ)
给定一个非空二叉树的根节点 root , 以数组的形式返回每一层节点的平均值。与实际答案相差 10-5 以内的答案可以被接受。
示例 1:

输入:root = [3,9,20,null,null,15,7]
输出:[3.00000,14.50000,11.00000]
解释:第 0 层的平均值为 3,第 1 层的平均值为 14.5,第 2 层的平均值为 11 。
因此返回 [3, 14.5, 11] 。
|
示例 2:

输入:root = [3,9,20,15,7]
输出:[3.00000,14.50000,11.00000]
|
提示:
-2^31 <= Node.val <= 2^31 - 1
和上一题一样, 层序遍历. 遍历每一层的节点, 统计节点的和, 每一层遍历完之后, 再计算平均值
class Solution {
public List<Double> averageOfLevels(TreeNode root) {
List<Double> res = new ArrayList<>();
Queue<TreeNode> que = new LinkedList<>();
que.offer(root);
while (!que.isEmpty()) {
double sum = 0;
int len = que.size();
for (int i = 0; i < len; i++) {
TreeNode node = que.poll();
sum += node.val;
if (node.left != null) {
que.offer(node.left);
}
if (node.right != null) {
que.offer(node.right);
}
}
double ave = sum / len;
res.add(ave);
}
return res;
}
}
|
lc102. 二叉树层序遍历(MD)
给你二叉树的根节点 root ,返回其节点值的 层序遍历 。 (即逐层地,从左到右访问所有节点)。
示例 1:

输入:root = [3,9,20,null,null,15,7]
输出:[[3],[9,20],[15,7]]
|
示例 2:
示例 3:
提示:
- 树中节点数目在范围
[0, 2000] 内 -1000 <= Node.val <= 1000
还是老样子, 数组+队列
class Solution {
public List<List<Integer>> levelOrder(TreeNode root) {
List<List<Integer>> res = new ArrayList<>();
if (root == null) {
return res;
}
Queue<TreeNode> que = new LinkedList<>();
que.offer(root);
while (!que.isEmpty()) {
int len = que.size();
List<Integer> tmp = new ArrayList<>();
for (int i = 0; i < len; i++) {
TreeNode node = que.poll();
tmp.add(node.val);
if (node.left != null) {
que.offer(node.left);
}
if (node.right != null) {
que.offer(node.right);
}
}
res.add(tmp);
}
return res;
}
}
|