Yonagi's Sekai
美团2023年秋招第一场笔试 个人题解
美团2023年秋招第一场笔试 个人题解
•
4 min read
Categories: 技术
Tags: C++ / 算法 / leetcode / 笔试

以下题解为个人题解，仅提供大致思路和提供题解代码。本题解使用的编程语言为C++。本次笔试为模拟测试，得分70.5/100，ac数7/9。题解内容仅供参考

美团2023年秋季校园招聘 第一场笔试【技术类】 题解（C++）

T1. 小美的外卖订单

小美正在设计美团外卖的定价信息。已知外卖定价的规则如下：

  1. 每道菜有折扣价和原价。折扣价不能超过原价。

  2. 订单有满 𝑥𝑥 元减 𝑦𝑦 元的优惠。当购买的菜的价格总和不小于 𝑥𝑥 元时，总价格可以减 𝑦𝑦 元。“减”的价格不能超过“满”的价格。

  3. 满减优惠和折扣价是互斥的，当且仅当每个菜都选择了原价才可以触发满减。

  4. 系统会自动为客户计算最低价格的方案。

在设计定价时，原价、折扣价和满减的价格都必须是正实数。如果设计的定价发生问题，则会提示数据错误。

请使用等价划分法设计测试用例，来测试该系统的功能。

时间限制：C/C++ 1秒，其他语言2秒

空间限制：C/C++ 256M，其他语言512M

输入描述：

第一行输入一个正整数n，代表菜的总数。
接下来的n行，每行输入两个实数ai和bi，代表每道菜的原价是ai，折扣价是bi。
最后一行输入两个实数x和y，代表满元可以减元。
1 <= n <= 1e5
数据中所有实数的绝对值不超过1000。

输出描述：

如果数据有误，则输出一行字符串"error"。
否则输出一个小数，小数点后保留2位即可。该小数代表顾客购买了全部菜各一份时，订单的总价格。

示例1:

输入例子：
2
10 5.5
10 6.5
15 3
输出例子：
12.00
例子说明：
虽然触发了满15元减3元，但使用折扣只需要花12元，低于使用满减的价格（20-3=17），因此最终系统会为客户推荐折扣价。

示例2

输入例子：
2
10 5.5
10 6.5
20 10
输出例子：
10.00
例子说明：
触发满20元减10元即可。满减价优于折扣价。

示例3

输入例子：
2
10 10.25
10 3.5
20 4.5
输出例子：
error
例子说明：
折扣价高于原价，数据错误。

没啥难度，鉴定为纯纯的语法题

#include <bits/stdc++.h>
using namespace std;
const int maxn = 1e5 + 10;
double a[maxn], b[maxn];

void io() {
    cin.tie(0);
    cout.tie(0);
    ios::sync_with_stdio(false);
}

int main() {
    io();
    int n;
	double x, y;
    cin >> n;
    for (int i = 1; i <= n; i++) {
        cin >> a[i] >> b[i];
        if (a[i] < b[i] || a[i] <= 0 || b[i] <= 0) {
            cout << "error" << '\n';
            return 0;
        }
    }
    cin >> x >> y;
    if (x < y || x <= 0 || y <= 0) {
        cout << "error" << '\n';
        return 0;
    }
    double sum_manjian = 0, sum_zhekou = 0;
    for (int i = 1; i <= n; i++) {
        sum_manjian += a[i];
        sum_zhekou += b[i];
    }
    if (sum_manjian >= x) {
        sum_manjian -= y;
    }
    printf("%.2f", min(sum_manjian, sum_zhekou));
    return 0;
}

如果使用C++语言的话，最后记得用printf并且要控制一下输出的小数位数。 笔者写这道题的时候因为忘记控制小数位数为2位，所以最开始就wa了一发

T2. 小美的字符串匹配度

小美有两个长度为𝑛n只包含小写字母的字符串 𝑠𝑠 和 𝑡𝑡 , 小美定义“两个字符串的匹配度”为𝑖∈[1,𝑛]i∈[1,n]中𝑠𝑖=𝑡𝑖𝑠_𝑖=𝑡_𝑖的数量，例如”abacd”和”aabdd”的匹配度就是2。

现在你可以进行最多一次以下操作: 对于字符串𝑡𝑡，选择两个索引𝑖,𝑗𝑖,𝑗(1≤𝑖<𝑗≤𝑛1≤𝑖<𝑗≤𝑛)，交换𝑡𝑖𝑡_𝑖​和𝑡𝑗𝑡_𝑗​。

小美想知道，𝑠𝑠 和 𝑡𝑡 的最大字符串匹配度是多少？

时间限制：C/C++ 1秒，其他语言2秒

空间限制：C/C++ 256M，其他语言512M

输入描述：

第一行输入一个整数n
第二行输入一个长度为n的字符串s。
第三行输入一个长度为n的字符串t。

输出描述：

输出一个整数，s和t的最大匹配度。

示例1：

输入例子：
5
ababc
babac
输出例子：
3

先把两个字符串遍历一轮，计算在没有交换的情况下的字符串匹配度

对于没能匹配的字符，我个人考虑使用vector来存。遍历完数组之后，再把两个vector都遍历一次，就能得到存在交换的情况下最大的字符串匹配度了

#include <bits/stdc++.h>
using namespace std;
const int maxn = 1010;
typedef long long ll;

void io() {
    cin.tie(0);
    cout.tie(0);
    ios::sync_with_stdio(false);
}

int main() {
    io();
	int n;
	cin >> n;
	string s, t;
	cin >> s;
	cin >> t;
	int res = 0;
	vector<char> svec, tvec;
	for (int i = 0; i < n; i++) {
		if (s[i] == t[i]) {
			res++;
		} else {
			svec.push_back(s[i]);
			tvec.push_back(t[i]);
		}
	}
	int exchange = 0;
	for (int i = 0; i < svec.size(); i++) {
		for (int j = 0; j < tvec.size(); j++) {
			if (svec[i] == tvec[j]) {
				exchange = exchange < 1 ? 1 : exchange;
			}
			if (svec[j] == tvec[i]) {
				exchange = exchange < 1 ? 1 : exchange;
			}
			if (svec[i] == tvec[j] && svec[j] == tvec[i]) {
				exchange = exchange < 2 ? 2 : exchange;
				break;
			}
		}
	}
	cout << res + exchange << '\n';
	return 0;
}

T3. 小美的树上染色

小美拿到了一棵树，每个节点有一个权值。初始每个节点都是白色。

小美有若干次操作，每次操作可以选择两个相邻的节点，如果它们都是白色且权值的乘积是完全平方数，小美就可以把这两个节点同时染红。

小美想知道，自己最多可以染红多少个节点？

时间限制：C/C++ 1秒，其他语言2秒

空间限制：C/C++ 256M，其他语言512M

输入描述：

第一行输入一个正整数n，代表节点的数量。
第二行输入n个正整数ai，代表每个节点的权值。
接下来的n - 1行，每行输入两个正整数u, v，代表节点u和节点v有一条边连接。

输出描述：

输出一个整数，表示最多可以染红的节点数量。

示例1：

输入例子：
3
3 3 12
1 2
2 3
输出例子：
2
例子说明：
可以染红第二个和第三个节点。
请注意，此时不能再染红第一个和第二个节点，因为第二个节点已经被染红。
因此，最多染红 2 个节点。

这道题是一道典型的图论题，我自己是非常讨厌图论的，打比赛的时候碰到图论题都是直接丢给队友做，但是这道图论题硬要说的话其实真没那么难

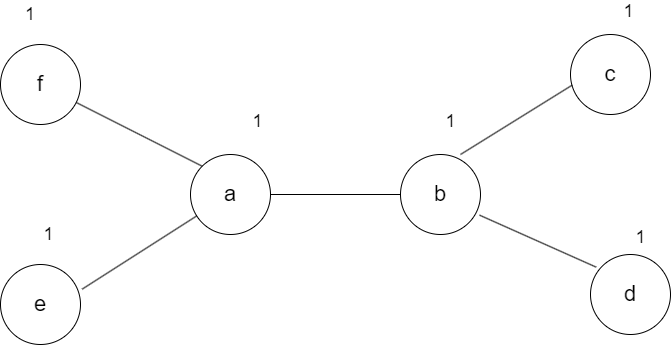
根据这张图可以知道，a和b是可以染色的，因为它们联通且它们的权值之积是完全平方，但是如果染了a和b，就无法给其他节点染色了。因此应当染上f-a或e-a和c-b或d-b。也就是染色要先从叶子节点开始染，如果把中间节点先染色了，那么很可能就没法继续染了

实现方法：先染外层节点，然后往内层节点推进。

#include <algorithm>
#include <bits/stdc++.h>
using namespace std;
const int maxn = 1e5 + 10;
typedef long long ll;
// 变量解释
// n：节点个数
// a：节点权值
// d：每个节点的边的数量
// red：是否被染色
// vis：是否遍历过
// e：图结构
ll n;
ll a[maxn], d[maxn], red[maxn], vis[maxn];
vector<int> e[maxn];

void io() {
    cin.tie(0);
    cout.tie(0);
    ios::sync_with_stdio(false);
}

// 完全平方判断
bool isPow(ll x) {
	ll y = (int)sqrt(x);
	return y * y == x;
}

int main() {
    io();
	cin >> n;
	ll res = 0;
	for (int i = 1; i <= n; i++) {
		cin >> a[i];
	}
	for (int i = 1; i <= n - 1; i++) {
		int u, v;
		cin >> u >> v;
		e[u].push_back(v);
		e[v].push_back(u);
		d[u]++;
		d[v]++;
	}
	queue<int> que;
	for (int i = 1; i <= n; i++) {
		if (d[i] == 1) {
			que.push(i);
		}
	}
	while (!que.empty()) {
		int x = que.front();
		que.pop();
		vis[x] = 1;
		for (int i = 0; i < e[x].size(); i++) {
			int y = e[x][i];
			if (vis[y]) {
				continue;
			}
			if (red[x] == 0 && red[y] == 0 && isPow(a[x] * a[y])) {
				red[x] = 1;
				red[y] = 1;
				res += 2;
			}
			d[y]--;
			if (d[y] == 1) {
				que.push(y);
			}
		}
	}
	cout << res << '\n';
	return 0;
}

T4. 小美的排列询问

小美拿到了一个排列。她想知道在这个排列中，xx 和 yy 是否是相邻的。你能帮帮她吗？

排列是指一个长度为 𝑛𝑛 的数组，其中 11 到 𝑛𝑛 每个元素恰好出现一次。

时间限制：C/C++ 1秒，其他语言2秒

空间限制：C/C++ 256M，其他语言512M

输入描述：

第一行输入一个正整数n，代表排列的长度。
第二行输入n个正整数ai，代表排列的元素。
第三行输入两个正整数x和y，用空格隔开。
1 <= n <= 200000
1 <= ai, x, y <= n
保证 x != y

输出描述：

如果x和y在排列中相邻，则输出"Yes"。否则输出"No"。

示例1：

输入例子：
4
1 4 2 3
2 4
输出例子：
Yes

示例2：

输入例子：
5
3 4 5 1 2
3 2
输出例子：
No

又是一道送分题，这是真送分啊（不过美团的笔试对面试的影响程度比较低，无论是ak还是一道题都没a出来都可以约面的（都会被泡池子），取决于投递的业务组）

#include <bits/stdc++.h>
using namespace std;
const int maxn = 200000 + 10;
int a[maxn];

void io() {
    cin.tie(0);
    cout.tie(0);
    ios::sync_with_stdio(false);
}

int main() {
    io();
    int n;
	cin >> n;
	for (int i = 1; i <= n; i++) {
		cin >> a[i];
	}
	int x, y;
	cin >> x >> y;
	for (int i = 1; i < n; i++) {
		if ((a[i] == x && a[i + 1] == y) || (a[i] == y && a[i + 1] == x)) {
			cout << "Yes" << '\n';
			return 0;
		}
	}
	cout << "No" << '\n';
    return 0;
}

T5. 小美的排列构造

小美定义一个数组 𝑎𝑎 的权值计算如下：

首先将 𝑎𝑎 的每一对相邻两项求和，得到一个 𝑏𝑏 数组。那么 𝑏𝑏 数组的最大值减最小值即为 𝑎𝑎 数组的权值。

例如，若 𝑎=[2,1,3]𝑎=[2,1,3]，那么 𝑏=[3,4]𝑏=[3,4]，𝑏𝑏 数组的极差是 11。因此 𝑎𝑎 数组的权值为 11。

现在小美希望你能构造一个长度为 𝑛𝑛 的排列，满足权值尽可能小。你能帮帮她吗？

排列是指一个长度为 𝑛𝑛 的数组，其中 11 到 𝑛𝑛 每个元素恰好出现一次。

时间限制：C/C++ 1秒，其他语言2秒

空间限制：C/C++ 256M，其他语言512M

输入描述：

一个正整数n，代表排列的长度。
2 <= n <= 200000

输出描述：

一个合法的排列。如果有多解输出任意即可。

示例1：

输入例子：
3
输出例子：
2 1 3
例子说明：
这个数组的权值为 1。输出[2,3,1]等排列也是合法的。

这道题是构造题。应付构造题其实没有什么特别好的办法，不像其他的题一样有一个大概的套路，最好的办法就是多写构造题，或者提高一点对数字的敏感度——即使是这样，有时候构造题也不一定能写出来。所以构造题可以很简单，也可以非常非常难

但是这道构造题算是简单的了——个人感觉这道题放进Codeforce最多就1000分段的题

什么是权值？aa 数组相邻两项的之和的最大最小之差就是权值。我们需要构造出权值最小的情况，那么就意味着我们需要尽可能构造出一种排列，使得 aa 数组的每相邻两项的和都应该靠近某个值。这道题的简单之处就在于数组无论怎么变换都是 nn 的全排列的一种情况，如果稍微变形一下，变成给定任意数组求该数组排列的最小权值，而且数组长度动辄1e5甚至1e7，那就很难了

那么我们用上一点灵性，就能想到一个点子——我们可以把最大最小值放在一起，这样每相邻的两项的和就接近于 n+1n + 1，最终得到的权值必然等于 11 。例如，对于数组 a=[1,2,3,4,5]a = [1, 2, 3, 4, 5]， 我可以将其变形为 a=[1,5,2,4,3]a = [1, 5, 2, 4, 3] ，这样得到的权值就等于 11 。这个地方可以用数学来证明，但是算法竞赛和笔试的时间往往不充裕，不允许我们进行数学证明，我们可以写几个样例来试一下这个思路到底是不是正确的

根据样例1，我们可以得到变形后的数组 a=[1,3,2]a = [1, 3, 2]，求出的权值就为 11 。读者可以尝试写出更多样例，最终还是会发现在 n>2n > 2 的情况下，数组 bb 的最小值是 n+1n + 1，最大值是 n+2n + 2，权值为 11 ；在 n=2n = 2 的情况下，权值就等于 33。但是经过我的实测，发现这道题并没有 n=2n = 2 的数据……作为边界条件居然不设一个数据，出题人要背大锅

#include <bits/stdc++.h>
using namespace std;
const int maxn = 200000 + 10;
int a[maxn];

void io() {
    cin.tie(0);
    cout.tie(0);
    ios::sync_with_stdio(false);
}

int main() {
    io();
    int n;
	cin >> n;
	int l = 1, r = n;
	for (int i = 1; i <= n; i += 2) {
		a[i] = l++;
		a[i + 1] = r--;
		if (l == r) {
			break;
		}
	}
	if (l == r) {
		a[n] = l;
	}
	for (int i = 1; i <= n; i++) {
		cout << a[i] << ' ';
	}
	cout << '\n';
    return 0;
}

T6. 小美走公路

有一个环形的公路，上面共有 𝑛𝑛 站，现在给定了顺时针第 𝑖𝑖 站到第 𝑖+1𝑖+1 站之间的距离（特殊的，也给出了第 𝑛𝑛 站到第 11 站的距离）。小美想沿着公路第 𝑥𝑥 站走到第 𝑦𝑦 站，她想知道最短的距离是多少？

时间限制：C/C++ 1秒，其他语言2秒

空间限制：C/C++ 256M，其他语言512M

输入描述：

第一行输入一个正整数n，代表站的数量。
第二行输入个正整数ai，前n - 1个数代表顺时针沿着公路走，i站到第i + 1站之间的距离；最后一个正整数n代表顺时针沿着公路走，第n站到第 1 站的距离。·
第三行输入两个正整数x和y，代表小美的出发地和目的地。
1 <= n <= 1e5
1 <= ai <= 1e9
1 <= x, y <= n

输出描述：

一个正整数，代表小美走的最短距离

示例1：

输入例子：
3
1 2 2
2 3
输出例子：
2

示例2：

输入例子：
3
1 2 2
1 3
输出例子：
2

不算难的模拟，记得写着写着不要把方向和距离是啥搞混了就行

还有就是这道题如果是用C++写的话，会爆int，记得开long long

#include <bits/stdc++.h>
using namespace std;
const int maxn = 1e5 + 10;
typedef long long ll;
ll a[maxn];

void io() {
    cin.tie(0);
    cout.tie(0);
    ios::sync_with_stdio(false);
}

int main() {
    io();
	int n;
	cin >> n;
	ll sum = 0;
	for (int i = 1; i <= n; i++) {
		cin >> a[i];
		sum += a[i];
	}
	int x, y;
	cin >> x >> y;
    if (x > y) {
        swap(x, y);
    }
    if (x == y) {
        cout << 0 << '\n';
        return 0;
    }
	ll l = 0, r = 0;
	for (int i = x; i < y; i++) {
		r += a[i];
	}
	if (r > sum / 2) {
		cout << sum - r << '\n';
	} else {
		cout << r << '\n';
	}
    return 0;
}

T7. 小美的好矩阵

小美定义一个矩阵是好矩阵，当且仅当该矩阵满足：

  1. 矩阵仅由’A’、‘B’、‘C’三种字符组成。且三种字符都出现过。
  2. 矩阵相邻的字符都不相等。

现在给定一个 𝑛×𝑚𝑛\times𝑚 的矩阵，小美想知道有多少个 3×33\times3的子矩阵是好矩阵，你能帮帮她吗？

时间限制：C/C++ 1秒，其他语言2秒

空间限制：C/C++ 256M，其他语言512M

输入描述：

第一行输入两个整数n, m，代表矩阵的行数和列数。
接下来的n行，每行输入一个仅包含大写字母的长度为m的字符串。
1 <= n, m <= 1000

输出描述：

输出一个整数表示答案。

示例1：

输入例子：
4 4
DABC
ABAB
BABA
BBAB
输出例子：
1
例子说明：
有4个3*3的子矩阵。
左上角的子矩阵出现了'D'，因此不合法。
右上角的是好矩阵。
左下角的存在两个相邻的字母相同，因此不合法。
右下角的子矩阵里没有'C'，因此不合法。

这道题我只过了样例……可能是我代码什么地方数组访问超界了，哎真的很可惜，这道题应该是一道比较简单的模拟题啊

不给代码了，网上的题解代码应该也不少

T8. 小美的蛋糕切割

小美有一个矩形的蛋糕，共分成了 𝑛𝑛 行 𝑚𝑚 列，共 𝑛×𝑚𝑛\times 𝑚 个区域，每个区域是一个小正方形，已知蛋糕每个区域都有一个美味度。她想切一刀把蛋糕切成两部分，自己吃一部分，小团吃另一部分。

小美希望两个人吃的部分的美味度之和尽可能接近，请你输出∣𝑠1−𝑠2∣∣𝑠1−𝑠2∣的最小值。（其中 𝑠1𝑠1 代表小美吃的美味度，𝑠2𝑠2 代表小团吃的美味度）。

请务必保证，切下来的区域都是完整的，即不能把某个小正方形切成两个小区域。

时间限制：C/C++ 1秒，其他语言2秒

空间限制：C/C++ 256M，其他语言512M

输入描述：

第一行输出两个正整数n和m，代表蛋糕区域的行数和列数。
接下来的n行，每行输入m个正整数a[i,j]，用来表示每个区域的美味度。
1 <= n, m <= 1e3
1 <= a[i, j] <= 1e4

输出描述：

一个整数，代表|s1 - s2|的最小值。

示例1：

输入例子：
2 3
1 1 4
5 1 4
输出例子：
0
例子说明：
把蛋糕像这样切开：
1 1 | 4
5 1 | 4
左边蛋糕美味度之和是8
右边蛋糕美味度之和是8
所以答案是0。

114514是吧，好臭的题面（哼哼啊啊啊啊啊啊）

（其实这道题最难绷的地方是题面样例数据是114514，然后题目要求计算”美味度之差“，太他妈搞了 ）(美味しかったです)（一三五红茶，二四六牡蛎，周日红茶，这就是美团homo的生活啊）

二维前缀和维护美味度，然后遍历二维前缀和的下边界和右边界就能得到最小的差值

还有一个经典老问题，就是这道题的一些数据求完总和会爆int，记得开long long

#include <algorithm>
#include <bits/stdc++.h>
using namespace std;
const int maxn = 1e3 + 10;
typedef long long ll;
ll a[maxn][maxn];
ll sum[maxn][maxn];

void io() {
    cin.tie(0);
    cout.tie(0);
    ios::sync_with_stdio(false);
}

int main() {
    io();
	int n, m;
	cin >> n >> m;
	for (int i = 1; i <= n; i++) {
		for (int j = 1; j <= m; j++) {
			cin >> a[i][j];
		}
	}
	for (int i = 1; i <= n; i++) {
		for (int j = 1; j <= m; j++) {
			sum[i][j] = (sum[i - 1][j] + sum[i][j - 1] - sum[i - 1][j - 1] + a[i][j]);
		}
	}
	int res = INT32_MAX;
	ll totalSum = sum[n][m];
	for (int i = 1; i <= m; i++) {
		ll left = sum[n][i];
		ll right = totalSum - left;
        if (abs(left - right) < res) {
            res = abs(left - right);
        }
	}
	for (int i = 1; i <= n; i++) {
		ll up = sum[i][m];
		ll down = totalSum - up;
		if (abs(up - down) < res) {
            res = abs(up - down);
        }
	}
	cout << res << '\n';
	return 0;
}

T9. 小美的字符串变换

这道题没写，时间不够了